|
RTDs are manufactured from metals whose resistance increases with temperature.
Within a limited temperature range, this resistivity increases linearly with temperature:
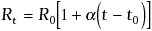 |
(2) |
where:
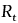 = resistance at temperature = resistance at temperature 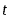
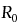 = resistance at a standard temperature = resistance at a standard temperature 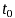
a = temperature coefficient of resistance (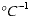 ) )
Combining Equations (1) and (2), setting 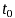 to 0°C, and rearranging to the standard linear y = mx+b form, it is clear that resistance vs. temperature is linear with a slope equal to a: to 0°C, and rearranging to the standard linear y = mx+b form, it is clear that resistance vs. temperature is linear with a slope equal to a:
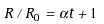 |
(3) |
In theory, any metal could be used to measure temperature. The metal selected should have a high melting point and an ability to withstand the effects of corrosion. Platinum has therefore become the metal of choice for RTDs. Its desirable characteristics include chemical stability, availability in a pure form, and electrical properties that are highly reproducible.
Platinum RTDs are made of either IEC/DIN grade platinum or reference grade platinum.
The difference lies in the purity of the platinum.
The IEC/DIN standard is pure platinum that is intentionally contaminated with other platinum group metals.
The reference grade platinum is made from 99.999+% pure platinum. Both probes will read 100Ω at 0°C, but at 100°C the DIN grade platinum RTD will read 138.5Ω and the reference grade will read 139.24Ω in RdF's maxiumum performance strain-free assemblies. International committees have been established to develop standard curves for RTDs. Only platinum RTDs have an international standard. Standards for any other metal are local. The committees have adopted a mean temperature coefficient between the 0°C and 100°C resistance values as the (“alpha”) for industrial platinum RTDs conforming to the relationships below.
Solving Equation (3) for a:
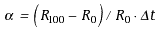 |
(4) |
IEC/DIN grade platinum: a = 0.00385 Ω/Ω/°C
Reference grade platinum: a = 0.003926 Ω/Ω/°C (max.)
The relationship between resistance and temperature can be approximated by the Callendar-Van Dusen equation:
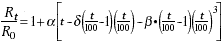 |
(5) |
where:
t = temperature (°C)
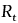 = Resistance at temperature t = Resistance at temperature t
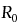 = Resistance at the ice point = Resistance at the ice point
a = Constant “alpha”, equation (4), (gives the linear approximation to the R vs. t curve)
d = Constant “delta” (for small 2nd order nonlinearity) (~1.5)
b = Constant “beta” (b = 0 when t is > 0°C) (opposes d ≤0°C, negligible effect above
–40°C) (~0.11)
The actual values for the coefficients a, d, and b are determined by testing the RTD at four temperatures and solving the equations.
The Callendar-Van Dusen equation was constructed to directly use laboratory data fixing alpha from 0°C and 100°C resistances. It is arranged from the prefered computation form used in the IEC/DIN International curve defining equation:
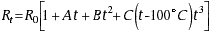 |
(6) |
In the positive quadrant, temperatures over 0°C, C is zero so the behavior of a platinum RTD simplifies to equation (7) which is also adequate for extrapolation to –40°C.
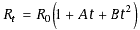 |
(7) |
As written, the above implies that valid equations for positive temperatures may be generated from empirical data taken using 0°C plus two arbitrarily selected positive temperatures. For a single PRT, the constants A and B could be slightly different, depending on the temperatures selected.
Callendar resolved the issue by defining two additional fixed points:
• The boiling point of water, 100°C (As embedded in equation (5) and (6))
• The freezing point of zinc, 419.53°C (Practical calibrations use >200°C)
The coefficients A, B, and C depend on the platinum material, purity, form (film or wire) and method of support. International standard IEC 751 defines them to permit universal interchangeability among international grade platinum RTDs.
The coefficients and their relationship to constraints in equation (5) are:
( C = 0 when 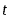 is > 0°C ) is > 0°C )
Only the a or A constants from 0°C and 100°C calibrations are needed to define individual probe curves in most applications where precision better than standard interchangeablitiy is desired. The other constants usually can be considered invarient in the range –100°C to 250°C. Only outside this range can differences exceed ordinary test precision on RTDs of the same type, requiring additional high and/or low test points.
|




